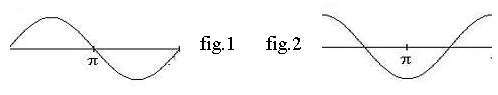
The tone of an organ starts swelling, but the hammer of a piano causes a sudden start (fig.2).
Sound (also the difference between a, e, i, etc) is determined by
overtones. To understand this we first must know what a sine is. This
occurs when a spinning circle is converted to an up and down motion. It
is the reverse of what a crankshaft in a motor does with the motion of
the piston. If the cone of a loudspeaker moves according to a sine it will
give the sound of a sine wave (fig.1). This tone is smooth, not rough or
course.
The tone of an organ starts swelling, but the hammer of a piano
causes a sudden start (fig.2).
An overtone is a sine wave with a frequency of a 2-, 3- or more fold of the frequency of the root. A string or organ pipe automatically makes overtones which are whole multiples of the root frequency. The overtones (also called harmonics) are added to the root. The first 7 overtones of c1 are respectively c2 g2 c3 e3 g3 b-flat3 c4. The loudness of the overtones decreases as they are higher, with the result you may hear a bass wire give a major chord but not a seventh chord any more.
The table click here for the table gives the frequencies of the piano tones (column 3) and those of the overtones of the bas note a0 (column 4). Column 5 shows the whole multiples of the root. Violinists use the frequencies of the overtones, but the piano is unable to do that. Its fault is put in column 6.
In column 7 you can see the frequency ratios of the major third and major triad is unambiguously defined, but the minor third has two possible definitions and the whole step even three: 7/8, 8/9 and 9/10. The whole step is especially expressed in the dominant seventh chord. Study shows it is this application that leads to the ratio 8/9. Furthermore the table shows the piano is remarkable good for this application as 8/9=0,888 and the piano has fore the ratio of a whole step 0,891. Some calculation will show this difference is small compared to that with the other two definitions of the whole step. Those two other ones are nice too, but not ideal as a leading note to the subdominant.
A piano sound is harder to reproduce by audio equipment than the
sound of an organ. If you suppose the volume of an organ tone starts
from zero and the piano gives all sine waves of the roots and overtones
by the stroke of the hammer suddenly at top volume figures 3 and 4
show this is no wonder. They have the graph of a simultaneous touch of
the notes c, e and g each with two overtones. Fig.3 shows the organ and
fig.4 the piano. The graph of the piano immediately after the stroke of
the hammer is more asymmetrical and has peaks till outside the
figure.
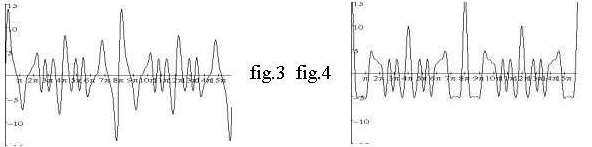
y(orgel)=(3*sin(x)+2*sin(2*x)+sin(3*x)+3*sin(1.25*x)+2*sin(2.5*x)+sin(3.75*x)+3*sin(1.5*x
)+2*sin(3*x)+sin(4.5*x) )
y(piano)=(3*cos(x)+2*cos(2*x)+cos(3*x)+3*cos(1.25*x)+2*cos(2.5*x)+cos(3.75*x)+3*cos(1.
5*x)+2*cos(3*x)+cos(4.5*x) )
A piano tuner tries to give all fifths an equal fluctuation. So the simultaneous sound of the notes c3 and g3 must have the same slow fluctuation in beats per second as the notes a4 and e4. The advantage of this equality is one can play in any key, but the disadvantage is the beats per second of a chord is different for a piano and for tones according to overtones (harmonics).