y(orgel)=(3*sin(x)+2*sin(2*x)+sin(3*x)+3*sin(1.25*x)+2*sin(2.5*x)+sin(3.75*x)+3*sin(1.5*x )+2*sin(3*x)+sin(4.5*x) )
y(piano)=(3*cos(x)+2*cos(2*x)+cos(3*x)+3*cos(1.25*x)+2*cos(2.5*x)+cos(3.75*x)+3*cos(1. 5*x)+2*cos(3*x)+cos(4.5*x) )
Een boventoon is een sinus van 2-, 3- of meervoudige frequentie. Een snaar of orgelpijp maakt vanzelf hele veelvouden van de grondfrequentie als boventonen, ook wel harmonischen genoemd. Boventonen worden bij de grondtoon opgeteld. De eerste 7 boventonen van c1 zijn achtereenvolgens c2 g2 c3 e3 g3 bes3 c4. Ze zijn naarmate ze hoger komen zo veel zwakker dat je in een bassnaar nog wel een majeurakkoord kunt horen, maar eigenlijk geen septimeakkoord meer.
Op de tabel (klik hier voor de tabel) staan de frequenties van de pianotonen (kolom 3) en die van de boventonen van de bas a0 (kolom 4). Kolom 5 toont de hele veelvouden van de grondfrequentie. Violisten gebruiken de frequenties van boventonen, maar de piano kan dat niet. Zijn fout staat in kolom 6.
In kolom 7 is te zien dat de frequentieverhoudingen van de grote terts en het majeurakkoord eenduidig vastliggen, maar dat er voor de kleine terts twee mogelijkheden zijn en voor de hele toonafstand zelfs drie: 7/8, 8/9 en 9/10. De hele toonafstand komt speciaal tot uitdrukking in het dominantseptimeakkoord. Als je het uitzoekt blijkt dat die septimetoon leidt tot de verhouding 8/9. Voorts blijkt de piano daar opmerkelijk goed in te zijn, want 8/9=0,888 en de piano heeft voor een hele toon de verhouding 0,891. Dat verschil is erg klein als je het vergelijkt met de andere twee definities van een hele toon. Die andere hele tonen zijn ook mooi, maar niet ideaal als leidtoon naar de subdominant.
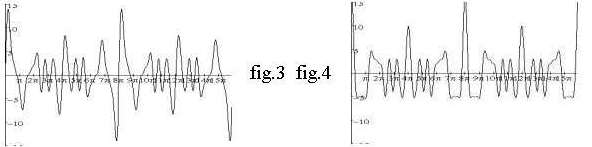
Een pianoklank is moeilijker met geluidsapparatuur weer te geven dan
een orgel. Als je aanneemt dat een orgeltoon aanzwelt vanuit nul en de
piano door de hamerslag alle tonen en boventonen op hun topsterkte laat
beginnen, kun je in figuur 3 en 4 zien dat dat begrijpelijk is. Die laten de
grafiek zien van de gelijktijdige aanslag van de tonen c, e en g ieder met
2 boventonen. Figuur 3 toont de klank van een orgel en figuur 4 van een
piano. De grafiek van de piano direct na de hamerslag is asymmetrischer en heeft
pieken tot buiten het beeld.

y(orgel)=(3*sin(x)+2*sin(2*x)+sin(3*x)+3*sin(1.25*x)+2*sin(2.5*x)+sin(3.75*x)+3*sin(1.5*x
)+2*sin(3*x)+sin(4.5*x) )
y(piano)=(3*cos(x)+2*cos(2*x)+cos(3*x)+3*cos(1.25*x)+2*cos(2.5*x)+cos(3.75*x)+3*cos(1.
5*x)+2*cos(3*x)+cos(4.5*x) )
Een pianostemmer probeert alle kwinten een gelijke zweving te geven. Dus de tweeklank c3-g3 moet dezelfde trage zweving hebben als a4-e4. Het voordeel van deze gelijkheid is dat in alle toonaarden gespeeld kan worden, maar het nadeel dat de tonen van samenklanken niet overeenstemmen met elkaars boventonen.